Welcome to RQL's Blog!
Do Better Every Day!-
大气位温、相当位温、饱和相当位温、静力稳定度
- 位温 potential temperature
- 相当位温 equivalent potential temperature
- 饱和相当位温 Saturation equivalent potential temperature
- 广义位温
- 静力稳定度
- 参考资料
位温 potential temperature
位温把干空气块绝热膨胀或压缩到标准气压(1000hPa)时的温度。在干绝热过程中具有守恒性,即一个气块的位温不随气块所处的高度或压强的改变而改变,而温度是非保守性的物理量,会随着气块的位置或压强的改变而变化。与温度相比位温是一种稳定的示踪物,方便我们追溯气块或气流的源地及研究他们以后的演变。
空气块受热位温上升,空气块放热时位温降低,干绝热过程位温保持不变
位温的垂直分布:在对流层内,一般大气的垂直减温率小于干绝热减温率,所以位温随高度增加而增加。未饱和湿空气的位温计算公式:
ncl的计算:
opt = False theta = pot_temp(pres_Pa, temp_K, dim, opt) ;dim, The dimension of temp_K which corresponds to pres_Pa ;pres_Pa的单位用Pa ;opt这个选项目前还没有开发到,直接设为 False ;计算公式:theta = temp_K*(p0/conform(temp_K,pres_Pa,dim))^0.286 ;p0=100000.0使用该函数的时候,记得检查各变量的单位,必须使用函数要求的单位(Pa和K)。
若输入的温度为相当温度 equivalent temperature,则也可以计算相当位温,但感觉这样计算的相当位温同用函数
pot_temp_equiv计算的,会低估。相当温度可以用下面的代码计算:cpd = 1004. or 1005.7 ; specific heat dry air [J/kg/K] Lv = 2.5104e6 ; [J/kg]=[m2/s2] Latent Heat of Vaporization of Water r = mixing_ratio ; [kg/kg]; same size and shape as t teqv = t + (Lv/cpd)*r ; equivalent temperature相当位温 equivalent potential temperature
相当位温是某一高度的气团下降(或上升)至参照气压值的位置时,经过绝热膨胀(或收缩)以及所含的水汽全部凝结为水滴释出潜热后,所具有的温度。一般适用于饱和湿空气,在饱和湿绝热过程中守恒。
假相当位温是饱和(或未饱和)湿空气块在绝热上升(先是干绝热上升到凝结高度,然后再湿绝热上升)过程中,在气块本身维持饱和的状态下,凝结出来的液态水立即脱离上升气块,直到该空气块所具有的水汽全部凝结完毕并脱落以后,该空气块所具有的位温。
假相当位温在干、湿绝热过程中均是保守的,因此天气学上常用它作气团和锋面的分析。 ——《大气物理学》 盛裴轩 假相当位温在对流层中低层主要反映了大气的湿度场特征;在中高层则主要反映温度对比。 ——(柳俊杰,2003)
个人感觉相当位温和假相当位温是同一个物理量,都是把温度、气压、湿度包括在一起的一个综合物理量。在ncl中,计算相当位温的函数的计算过程等同于假相当位温。
对于干绝热、湿绝热、假绝热过程,假相当位温都保持守恒。
ncl的计算:
;利用抬升凝结温度计算相当位温 theta_e = pot_temp_equiv_tlcl(pres, temp, tlcl, mixr, iounits) ;tlcl抬升凝结温度的单位同temp温度,四个数组的维数最好一样吧 ;iounits是有四个数值的一维数组,用来说明各变量单位 ;输出结果的维数同temp ;抬升凝结温度的计算有四种方法(就是用四种不同的变量计算tlcl) tlcl = tlcl_mixr_bolton(temp, mixr, p, iounits) ;利用混合比计算tlcl tlcl = tlcl_rh_bolton (temp, rh, iounits) ;利用相对湿度计算tlcl tlcl = tlcl_evp_bolton (temp, evp, iounits) ;利用水汽压计算tlcl tlcl = tlcl_td_bolton (temp, td, iounits) ;利用露点温度计算tlcl ;函数中的所有数组的维数必须相同 ;不用抬升凝结温度,直接估算相当位温,据说会存在系统性低估 theta_e = pot_temp_equiv(pres_Pa, temp_K, water, dim, humVarType) ;dim表示temp_K中的哪一维同pres_Pa,若这两个变量的维数相同,dim=-1 ;humVarType是一个字节变量,表示water中具体选用哪一个与水汽有关的物理量,"r"表示用比湿(kg/kg)因此,计算假相当位温需要变量:气压、温度、混合比(可以用比湿换算)。
关于各水汽变量的概念,参考这篇博文 https://renqlsysu.github.io/2018/02/23/about-water-vapour/饱和相当位温 Saturation equivalent potential temperature
当空气处于饱和状态时计算得到的相当位温。在相同温度和压强情况下,饱和相当位温大于相当位温。
广义位温
位温适用于干空气,相当位温适用于饱和湿空气,那么广义位温适用于未饱和的湿空气状态,由曹洁和高守亭于2008年提出,计算公式如下:

感觉这个不如假相当位温好用
静力稳定度
静力稳定度由密度或位温的垂直分层情况所决定的,单位:K/Pa
本来研究位温的计算就是为了计算静力稳定度(或对流不稳定指数),结果发现ncl就有计算静力不稳定的函数,所以一起看一下吧。发现输入的数据同位温函数
pot_temp的计算。sopt = 1 s1 = static_stability(press_Pa, temp_K, dim, sopt) ; explicitly extract each variable from the list S1_s = S1[0] ; static stability S1_pt = S1[1] ; theta S1_dthdp = S1[2] ; d(theta)dp ;The dimension of temp_K which corresponds to pres_Pa ;sopt=0, Return static stability only ;sopt=1, Return static stability, theta, d(theta)dp as type list ;使用的公式是 s = -T*d[log(theta)]/dp = -(T/theta)*d(theta)/dp参考以下文献,静力稳定度指数可以用925hPa和600hPa的相当位温之差表示,值越大表明大气越不稳定。对流不稳定指数可以用925hPa的相当位温与500hPa的饱和相当位温之差。差值为正,表示对流不稳定。
Sampe, T. and S.-P. Xie (2010). Large-Scale Dynamics of the Meiyu-Baiu Rainband: Environmental Forcing by the Westerly Jet. Journal of Climate. 23: 113-134.
参考资料
- https://baike.baidu.com/item/%E4%BD%8D%E6%B8%A9
- https://baike.baidu.com/item/%E5%81%87%E7%9B%B8%E5%BD%93%E4%BD%8D%E6%B8%A9
- https://baike.baidu.com/item/%E7%9B%B8%E5%BD%93%E4%BD%8D%E6%B8%A9
- http://glossary.ametsoc.org/wiki/Saturation_equivalent_potential_temperature
-
ncl相关系数的计算函数
esccr(x,y,mxlag)计算x和y最右边维的交叉时滞相关,0 <= mxlag <= N/4。如果要算超前滞后相关,需要进行两次运算,如下所示:mxlag = 9 x_Lead_y = esccr(x,y,mxlag) y_Lead_x = esccr(y,x,mxlag) ; switch the order of the series ccr = new ( 2*mxlag+1, float) ccr(0:mxlag-1) = y_Lead_x(1:mxlag:-1) ; "negative lag", -1 reverses order ccr(mxlag:) = x_Lead_y(0:mxlag) ; "positive lag"esacr(x,mxlag),计算时滞自相关系数escorc(x,y),只能计算Pearson同时线性交叉相关run_cor(x,y,time,wSize),计算滑动相关。使用该函数需要调用一个脚本:load "$NCARG_ROOT/lib/ncarg/nclscripts/contrib/run_cor.ncl"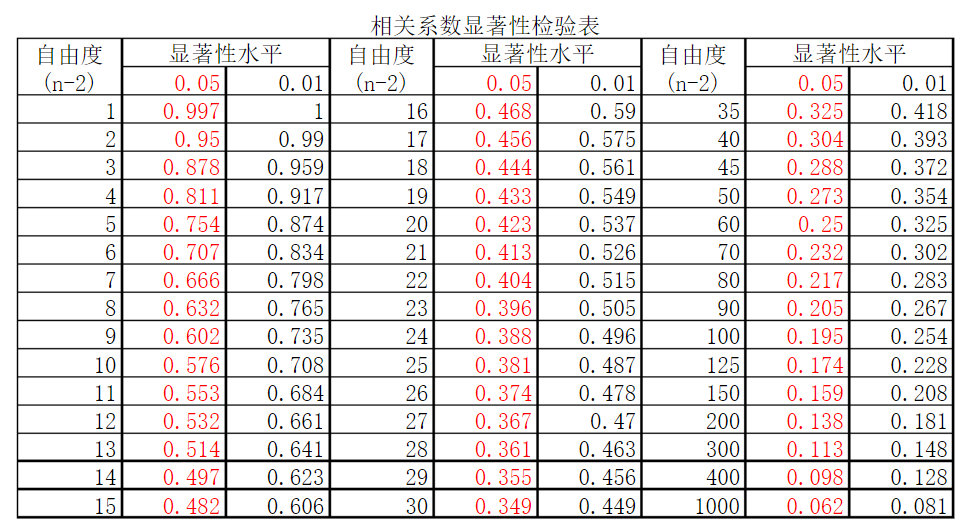
-
《混沌的本质》
《混沌的本质》是Lorenz写的书的中文译本,属于高级科普读物,1997年出版中文译本。Lorenz于60年代研究天气预报理论时发现混沌现象,被誉为混沌之父,提出蝴蝶效应。
混沌最初表示完全缺乏具体形态或系统排列,后常用来表示某种应该有的秩序却没有出现,一般代表随机性、杂乱无章。- 混沌在本书中是一种确定的系统中出现的无规则运动。他们看起来时随机发生的而实际上其行为却由精确的法则决定。称作貌似随机。即看起来像而实质上不是随机的事物。
- 混沌理论研究的是非线性动力学混沌,目的是揭示貌似随机的现象背后可能隐藏的简单规律,以求发现一大类复杂问题普遍遵循的共同规律。
狭义的随机性定义:一个随机序列应满足,随时可能发生的任何事件在下个时刻也可能发生。即某特定事件在下一时刻发生的概率等于其在此后任一时刻发生的概率。
广义的随机性定义:允许一个随机序列中下一时刻的可能事件与刚发生过的事件有关,但下一时刻发生的事情有很多种可能性。同时不要求过去可能发生的任何事件也可在下一时刻发生。
确定性序列则认为下一时刻只可能发生一件事,且该事由上一时刻决定,即其演变由精确的法则决定。在任何系统中,对初始条件的敏感的依赖性所导致的直接结果之一是不能作准确预报,而对充分遥远的未来甚至连粗略预报都不可能。因为我们不能获得完全无误的观测。
当某一系统中互不相识的状态数目有限,必能出现任意接近的的重现状态的系统被称为系统的紧致性。缺乏周期性不等于混沌,也有可能是这个系统缺乏紧致性。但一个紧致系统既非周期也非准周期,那他就应是混沌的。
一个命题的陈述是否正确往往取决于其中各个用词是怎样定义的。显然,要就某种现象发展一套严谨的理论,就应先给出有关现象的毫不含糊的定义。
虽然还只是看了个开头,但大致可以看出Lorenz的观点是,虽然大气是混沌的,但依旧具有可预报性。虽不能百分之百的预报准确,但可以尽量地提高预报准确性。
Lorenz认为当时预报误差主要来自于我们对大尺度天气过程特征结构的不完全观测、、控制大气运动的物理规律的了解不够充分、计算时引入的近似。而小尺度特征结构如单个云的位置等观测误差还不是主要的。
Lorenz认为巴西一只蝴蝶翅膀的拍打不能对美国德克萨斯州的龙卷产生显著影响。
-
《亚洲季风》引言翻译
最近在老板和其他任课老师的熏陶下,准备读一下王斌老师2006年出的一本关于季风的书 《The Asian monsoon》。从目录上来看,感觉这本书包含的内容相关全面。 一共有800多页,是个相当浩大的工程,不知道是否能完成。不管如何,先看个引言再说吧。
Preface
亚洲季风是地球气候系统中一个壮观的景象。
夏季,季风从印度洋和太平洋抽吸水汽,在南亚和东亚产生强降水。同时在亚洲北部和西部导致下沉的干空气,造成全世界最大的干旱地带。
冬季,西伯利亚冷高压将空气输送到南半球,在印度尼西亚、北澳大利亚、南支ITCZ处产生强降水。那么是什么导致亚洲季风如此强大?目前的观点认为是世界上最大的陆地(欧亚大陆)和最大的海盆(印度-太平洋)之间的热力对比,加上世界最高脊的存在。
这种特殊的地形配合太阳辐射的年循环以及地球自转效应产生风场和降水在冬夏季节反相的季风气候。
水循环过程又进一步放大这种季风环流。副热带地区的沙漠以及地中海气候往往被认为是由季风环流引起的副作用。巨大的亚洲季风系统(也叫亚欧季风系统)控制了整个东半球的热带和副热带。它与ENSO、热带外环流相互作用,对全球气候和环境都有影响。亚洲季风系统作为地表、海洋、大气、水文和生物圈相互作用最强烈的例证,具有不可忽视的科研意义。
-
简单模式动力设置和几种修改方法
发现有很多跑简单模式的文献,准备收集整理一下,以资参考。
Held-Suare 1994年的基本设置
Held, I. M. and M. J. Suarez (1994). “A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models.” Bulletin of the American Meteorological Society 75(10): 1825-1830.
觉得如果要修改CESM干模式的动力核,还是有必要把这篇经典的文章再读一遍。
为了评估大气环流模式独立于物理参数化的动力核,该文设计了一个基准实验。这个实验关注模式结果的长期统计特征,因此非常适合于气候模式的动力核比较 为了说明这个基准实验的用处,两个完全不同的大气动力核(谱模式、差分格式)用于比较。
利用牛顿松弛方法来施加强迫,当温度低于给定的辐射平衡温度时加热,反之则冷却。同时在风场底层(sigma>0.7的地方,sigma值为1时代表地表)用瑞利阻尼的方法来模拟边界层摩擦效应。

其中辐射的松弛时间(Ka或者Ks的倒数)也是一个关于纬度和高度的函数,在sigma<0.7也就是大气内部,松弛时间是40天,而赤道地区近地表的松弛时间最短是4天。如果各个地方都用统一的松弛时间,那么会在近地表区域产生一个不真实的薄冷层,尤其在赤道地区。因此赤道地区的松弛系数较大(即松弛时间短),以减弱这种效应。
那么为什么会在底层产生一个不真实的冷区呢?我的猜想是:在没有地表摩擦消耗时,因为赤道的辐射平衡温度高,本身就存在环流。而地表摩擦的存在使得底层的能量存在耗散,为了维持环流的存在,就必须使地表温度弱于辐射平衡温度,以产生加热。

实验的目的不是为了产生了真实的大气环流,而是为了在可解析的所有尺度上更好地模拟大气运动。
Schneider 2008年 加入辐射强迫的年循环
Although the resulting Newtonian temperature relaxation rate is not easily justifiable as a radiative heating rate, we will call it, for simplicity, a radiative heating rate



-
ENSO Dynamics
海洋基础知识
- 温跃层thermocline、盐跃层halocline以及密度跃层pycnocline三者等价。据此可以把海洋分为表层(也叫混合层)、突变层和深层三层,且海洋的三层结构非常稳定,不像大气那样易发生对流。此外,三层结构在低纬非常明显,高纬的结构则没有那么明显。可能是因为高纬地区的海洋表层海温与深层海温近似,热带则相差较大。突变层不利于海水的垂直运动。
- 海洋混合层厚度在夏季晚期最薄,因为夏季的风小,加上太阳辐射强,使得海洋表层温度高,不利于混合,因此混合层薄。反之,冬季晚期混合层最厚。
- 大西洋结构与太平洋类似,都有暖池和冷池,但为什么太平洋有ENSO,而大西洋没有呢?是因为太平洋的海盆面积比较大吗?还是因为大西洋主要是温盐环流占主导?
- 大西洋多年代际振荡与温盐环流密切相关。一般在说到温盐环流时多聚焦于大西洋,而风生环流则多在太平洋,为什么?大西洋的盐度比太平洋高?
- 海洋对大气的影响主要是潜热,而大气对海洋的影响主要是风应力(Ekman Transport)。海气相互作用最强的地方并不等于蒸发最强的地方。
- 海洋有低反照率、高比热容,使其能存储更多的能量。加上近海面大气含有丰富水汽,使海表面发射的长波辐射被截留在海表面附近
- 为了简化,海洋模式多用混合层模式来替代整个海洋模式

- Ekman Transport 是发生在海洋表层的海水运动,受风应力和科氏力的作用。北半球,Ekman流偏向风应力的右边。因此热带海水由于赤道信风的Ekman抽吸而存在上升辐散运动,温跃层抬升,底层Sverdrup是向赤道流,构成一个海洋里的经向环流,该经向环流有利于海洋热量的向极输送。
- Sverdrup Transport 发生在海洋深层,相当于补偿流,用于补偿由Ekman输送造成的空缺,是海洋中的准地转流。虽然也有一种成因是说该深层流的产生是因为涡度的变化(温跃层因Ekman流而抬升,根据位涡守恒,其绝对涡度需要增加,但由于深层流本身不会旋转(相对涡度为0),因此它只能通过向极运动来使地转涡度增大)。且也有提到说,Sverdrup的辐散辅合区与Ekman输送导致的温跃层抬升或下降区是错位的
- 暖池(温度大于28℃)、冷舌(温度低于24℃)
