瞬变涡旋诊断量

折射指数
eddy的几种计算
瞬变涡旋诊断量意义
Eady growth rate
波活动通量算法参考

折射指数

在折射指数为正的区域，波动传播。
在折射指数为负的地方，波动容易消散。
且波动倾向于往正反射指数大的区域传播。

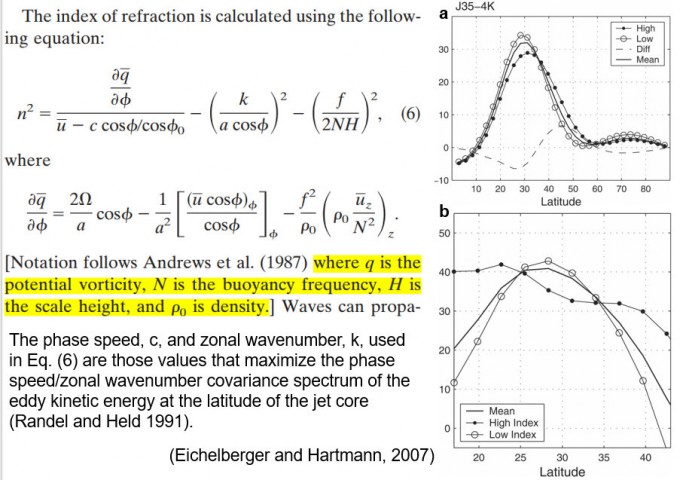
上面图a与图b分别显示的是不同情况下的纬向平均U风和折射指数的合成图。
在high index时，急流强度减弱且变得更宽，此时波动向赤道移动，离开了波动源（即eddy-driven jet区域），有利于产生eddy momentum fluxes，进而通过波流相互作用维持西风急流异常。
在low index时，急流变窄且增强，此时折射指数在波动源区达到最大，意味着波动难以离开波源，不利于eddy momentum fluxes的产生，使得波流相互作用减弱，难以维持西风急流异常。此时若计算两种情况下的eddy momentum fluxes，会发现high index的eddy momentum fluxes高于low index。该图也表明，当急流过强时，它就像一个波导，减弱了波动的径向传播，波流相互作用减弱。

eddy的几种计算

逐日数据减去当年季节平均或当年月平均，这样处理的异常包含2-90天或2-30天的瞬变波动
逐日数据减去气候态季节平均或气候态月平均，或者气候态逐日年循环（用气候态年平均值+气候态逐日年循环的前四个Fourier谐波分量）。这样的瞬变异常中可能还包含年际异常，但该异常与瞬变异常相比较弱很多。也包含高低频瞬变波动
2-10天或2-7天滤波得到高频天气尺度瞬变，10-90天滤波得到低频波动。该滤波可以基于原始数据（滤波时会减去平均值），或者方法1方法2计算得到的anomaly

上述几种计算方法得到的EKE大值区基本一致，只是大小会因为包含的频率范围而有差异。此外还有基于时间平均纬向平均的异常，这包含瞬变和定常波动。也可根据纬向空间滤波。

其中前四个Fourier谐波分量的提取常用ezfftf和ezffeb两个函数，而滤波可以用bw_bandpass_filter,具体见我的另一篇博文。

瞬变涡旋诊断量意义

涡旋能量是一个客观、具有物理动力意义的诊断量，包含瞬变涡旋动能EKE和瞬变涡旋有效位能EAPE。其中EKE可以直接反应涡旋环流变率，而EAPE则代表了与气象事件有关的温度波动。
EP通量只能用于全球纬向平均的二维平面上，等于Rossby群速乘以波活动密度，其辐合辐散也代表局地波活动密度的增加减少。此外，其辐合辐散也可以代表由eddy贡献的纬向平均的径向位涡通量，在EP通量辐合处，有向南的异常位涡的异常输送。由于EP通量可以表示波活动密度的传播，其中eddy heat flux与波活动的垂直通量成正比，因此可以用底层eddy heat flux来表征垂直波活动通量的变化。而时间平均的eddy动量通量散度的变化可能是因为地表向上的波活动通量减少或者从波源向外传播的波活动减弱。
E矢量可以作为二维EP通量的扩展，其辐合或辐散代表着波活动密度的增加或减少。其方向代表着相对于平均流的Rossby波群速或波动能量传播速度。其辐合辐散也能诊断波流相互作用，在E矢量辐合处，西风风速降低。此外，E矢量水平分量与时间平均纬向风速的水平梯度的点乘与平均流和扰动场的局地正压能量转换率成正比，当点乘为正时，存在正的能量转换，通过从平均流向eddy的正压动量转换减弱纬向风场的不均一性。E矢量的垂直分量（即瞬变热量输送）在高层很弱，因此在高层可以只考虑水平分量。其x分量可以反映波动形状。
波活动通量 WAF，它能根据背景流来量化波能量传播。可以在背景流存在纬向变化情况下，明确描绘瞬变涡旋的传播，其方向于Rossby波群速平行。其辐散或辐合也意味着波包的源或汇。

顺便再解释一下有效位能的概念：即可以转化为动能的全位能（内能和重力位能之和），指系统的全位能与该系统经绝热调整到正压及静力平衡状态（一种参考状态）时所具有的全位能（即最小全位能）之差，取决于等压面上的位温离差（相对于区域平均的异常）、温度离差或比容离差，即大气斜压性。一般来说有效位能约为全位能的二百分之一，且有效位能中只有大约十分之一转变成了动能。因此，若将大气视为一部由太阳辐射驱动的热机，太阳辐射能首先转变为大气全位能，然后再由全位能转变为大气运动的动能，其效率非常低。

中纬度，热量是顺梯度输送的，且一般都是将平均有效位能向扰动有效位能转换。动量是逆梯度输送（动量都向急流轴（动量大的区域）输送），此时将扰动动能转向平均动能。平均动能和平均有效位能之间通过垂直温度通量来转换，扰动动能和扰动有效位能之间通过扰动垂直温度通量来转换。如果一个环流在暖区域上升，冷区域下沉，那么是平均有效位能向平均动能转化（例如Hadley环流）。但如果是暖区域下沉，冷区域上升，那么是平均动能向平均有效位能转化（例如Ferrel环流）。全球实际大气中，大部分能量都是以平均全位能的形式储存。

在一个斜压波的生命周期内，在eddy初期，有扰动温度通量，能量从平均有效位能向扰动有效位能转化。在eddy后期，扰动动量通量强，能量从扰动动能向平均动能转化，急流增强。

下面是各诊断量的计算公式及效果图

参考来源：

Gu, S., Zhang, Y., Wu, Q., & Yang, X.‐Q. ( 2018). The linkage between arctic sea ice and midlatitude weather: In the perspective of energy. Journal of Geophysical Research: Atmospheres, 123, 11,536– 11,550. https://doi.org/10.1029/2018JD028743
贺海晏 2010年《动力气象学》第十章

Eady growth rate

Eady growth rate 是斜压最不稳定模态的线性增长速率，单位：1/s，也可转换为 1/day，是衡量斜压性或涡旋增长速率的一个常用指标，从Eady model (1949) 推导出来。其量级一般在 3x10^-6 s^-1 倒数一般与中纬度气旋的特征生命长度相吻合。其数值大小与静力稳定度成反比，与纬向风速的垂直切变即径向温度梯度成正比。

ncl有直接计算该诊断量的函数 eady_growth_rate (th, uwnd, hgt, lat, opt, lev_dim) ，但只适用于 ncl6.4.0版本及其以后，其计算公式如下：

eady_growth_rate = 0.3098*abs(f)*abs(du/dz)/N  

N**2 = g[d(lnθ)/dz] ;the Brunt-Vaisala frequency of atmosphere，also called buoyancy frequency
;当气块受到垂直扰动时，该气块振荡的频率，可以用来衡量稳定度
;当N**2大于0时，大气稳定；N**2小于0时，大气不稳定；N**2等于0时，大气中性
;大气重力内波的频率一般不会超过 local Brunt–Väisälä frequency
;也有文章认为这是大气静力稳定度，但个人觉得两者还是有些差别的，
;首先静力稳定度的单位是K/Pa，而N**2的单位是 s^-2
;N^2 的量级 10^-4 s^-2

;ncl有专门的计算Brunt-Vaisala frequency的函数
brunt = brunt_vaisala_atm(th, hgt, opt, ndim)
;hgt的单位是m，输出的结果是N（单位：1/s）
;opt=0, Return only the Brunt-Vaisala frequency as a regular variable.
;opt=1, Return the Brunt-Vaisala frequency and d(theta)/dz
;但用该函数计算得到的N可能为负，但这是不可能的，所以需要用下面的函数判断一下
brunt = where(brunt.lt.0.00000000001,0.00001,brunt)

由于Eady growth rate是一个非线性量，因此不能用月平均或年平均的量来直接计算。如果需要气候态的EGR，需要先用高频的变量（例如逐3h，逐6h，daily）来计算EGR，然后再算气候态。

发现用ncl的函数计算EGR比自己编程计算得到的对流层底层EGR小很多，这是因为ncl官网函数在计算过程中，将浮力频率为0的设为缺测，但保留了负的浮力频率，使得计算得到的EGR中有负值，因此气候态的EGR在某些对流不稳定地区就会偏小许多。而自己编程过程中，将负的浮力频率转换成了正值，于是那些经常有对流不稳定发生地区的EGR就会偏大（主要集中与西北太平洋、大西洋副极地地区）。但如果是把负的浮力频率也转换成缺测，那结果就与ncl函数类似。

; 用ncl自带的函数 eady_growth_rate 计算
opt = 0 ;opt=0, Return the Eady growth rate
;opt=1, Return the Eady growth rate and the vertical gradient of the zonal wind (du/dz)
;opt=2, Return the Eady growth rate and the vertical gradient of the zonal wind (du/dz) 
;        and the Brunt-Vaisala frequency

lev_dim = 1
lat = conform(air,vars&lat,2)
hgt = hgt/9.8 ;convert unit from m2/s2 to m
th  = pot_temp(lev*100, air, lev_dim, False) ；calc potential temperature
EGR = eady_growth_rate(th, uwnd, hgt, lat, opt, lev_dim)



; 根据公式自己写，结果几乎一样
lev_dim = 1
lat = conform(air,vars&lat,2)
pi = atan(1.0)*4
f0  = 2*(2*pi/24.0/3600.0)*sin(lat*pi/180.0)

;static = static_stability(lev*100, air, lev_dim, 0)
;static = conform(air,dim_avg_n(static,0),(/1,2,3/))
;static = where(static.lt.0.0000000001, 0.000001, static)

hgt   = hgt/9.8 ;convert unit from m2/s2 to m
theta = pot_temp(lev*100, air, lev_dim, opt)
brunt = brunt_vaisala_atm(theta, hgt, 0, lev_dim)
brunt = where(brunt.lt.0.00000000001,0.00001,brunt)

opt    = 0     ;used by center_finite_diff_n, no meanging
cyclic = False ;used by center_finite_diff_n
EGR  = 0.3098*(f0/brunt)*center_finite_diff_n(uwnd, hgt, cyclic, opt, lev_dim)

波活动通量算法参考

Nowadays，I am studying how to calculate the wave activity flux by ncl and its theory as well as its hypothesis.

Recommended by classmate，there is a website introducing the algorithm and procedure.

The algorithm of this website reference the following two papers：

Plumb, R. A. (1985). “On the three-dimensional propagation of stationary waves.” Journal of the Atmospheric Sciences 42(3): 217-229.

Takaya, K. and H. Nakamura (2001). “A formulation of a phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow.” Journal of the Atmospheric Sciences 58(6): 608-627.

其中，Pb85的文章是基于纬向平均的异常位势高度计算的，另外还用纬向平均的温度来计算位温。
TN01基于气候态平均的异常位势高度计算，另外还用到daily（or monthly） T, U, V

;  Gas constant
gc=290

;  Gravitational acceleration
ga=9.80665

;  Radius of the earth
re=6378388

; scale height
sclhgt=8000.

; pi
pi = atan(1.0)*4.
; cosine
coslat = cos(lat(:)*pi/180.)

准定常波活动通量的激发源主要有三个：

大地形扰动
绝热加热
与瞬变涡流相互作用，导致热量和动量的传输

计算过三种波活动通量（如果E矢量也算的话），现将计算过程中的一些注意点罗列一下。具体参考文献见另一篇博文几类波活动通量的文献调研

PB85定常波

主要用于定常波的分析，矢量Fs与Rossby波群速平行。在西风背景流下，Fs辐合代表波活动聚集（波汇），Fs辐散代表波活动的输出（波源）。z坐标系下，Fs的单位是m2/s2；p坐标系下，Fs的水平通量单位依然是m2/s2，垂直通量单位是Pa*m/s2，且负值代表向上的通量。计算时尽量用z坐标系吧，可以用p坐标系下的变量，只是将p坐标系通过 noz = -sclhgt*log(lev/1000.0) 直接转换成z坐标系。其实，z坐标系与p坐标系最大的不同在于垂直通量项，若不看垂直通量，影响不大。
由于是地转平衡假设，流函数可通过位势高度（单位m2/s2)除以科氏参数(单位s^-1）得到。当然也可以利用水平风速和球谐函数计算流函数（需要用到全球的数据），但这样比较麻烦，且对计算结果影响不大。
对于气候态定常波，扰动项是相对于纬向平均的异常。但若要分析与某现象有关的定常波，则可以用回归流函数作为扰动项，此时回归前流函数是否是相对于纬向平均的异常对结果影响不大。且计算结果与TN01版的波活动通量（也是用回归流函数作为扰动项）类似。基于TN01版本可以刻画纬向非均一背景下波动的传播特性，因此个人觉得此时用TN01版本会比较好。
一般，为了减少由多次微分导致的噪声放大，利用地转风和热成风关系将波活动通量公式改写为式（7.1）。但该式第一项似乎少乘了一个1/2。
利用式（7.1）计算ERA-interim 1979-2016年冬季气候态定常波，需要用到扰动风速(m/s)、扰动温度(K)和扰动位势高度（m2/s2)四个变量。结果发现在北太平洋中部存在向极的WAF，垂直通量分布比较散乱，但散度项分布相对连续，这与Pb85文章中的定常波不太一样，在想可能是因为现在的再分析数据中扰动温度、扰动风场及扰动位势高度没有满足准地转条件。
用式（5.7）计算ERA-interim 1979-2016年冬季气候态定常波，只需要用到位势高度和温度两个变量。此时北太平洋中部不存在向极的WAF，垂直通量分布比较连续，但散度项分布散乱。结果与Pb85文章中的例子类似，只是Pb85中的定常波WAF是基于方法3计算的。

TN01定常波or瞬变波

TN01版本的波活动通量与局地Rossby波的三维群速平行，因此可以用来描述纬向变化基本流上移动或定常涡旋的三维波包的瞬时传播特性。与PB85相比，该文波活动通量能更好地跟随基本流的蜿蜒，因此也能更好地代表定常Rossby波群速的平流效应。此外，在Plumb85中，波活动无法传播到纬向平均为东风的纬带；但TN01的波活动却可以在西风区域传播，即便该纬度纬向平均为东风。西伯利亚TN01的波活动通量的变化趋势总体大于Plumb85，是因为西伯利亚背景西风远远大于纬向平均。
单位同PB85。
若要研究瞬变涡旋的瞬时特征，扰动项是高频滤波后某一时刻的数据，然后利用高频滤波位势高度的超前滞后相关来估算每一点的相速Cp。具体见 TN01 WAF 实际应用
若要研究与某气候态现象相关的定常波，可以用回归的异常作为扰动项，计算得到的结果与PB85类似。若研究与某天气时间相关的定常波，可以挑选出该天气事件，然后合成，若该异常是逐日或逐6小时的，应当再做低通滤波来滤去更高频且移动的瞬变涡旋，再将滤波后的数据减去气候态基本态，将差值作为扰动项。此外，对于定常波，相速Cp可设为0。
但无法用该式来计算气候态定常波。曾尝试用每年冬季平均减去气候态冬季平均作为扰动流函数来计算气候态定常波，发现计算得到的WAF相对PB85定常波WAF较小。但方向同低频eddy的WAF类似，只是幅度小很多。且该方法的异常流函数乱码。
若要研究瞬变涡旋的气候态传播特性，可以用高频滤波后的流函数计算每天的WAF，再算气候态的WAF。

E vector

E矢量形式同EP通量，只是多了x方向的通量。单位同波活动通量的单位。
在其他地方都没有见过球坐标系下的E矢量公式，但在Vallis的书中提到了球坐标系下的EP通量，基于E矢量是EP通量的扩展形式，因此我将E矢量y和z方向的通量乘以coslat，从而计算全球E矢量。发现此时高纬度地区的垂直通量减弱很多，个人觉得比没乘coslat的合理些。
E矢量和瞬变涡旋的波活动通量分布存在明显不同，尤其是低频涡旋（E矢量中向西传，TN01中冬传），虽然二者都表现了瞬变Rossby波的群速。个人感觉TN01准确些，因为E矢量文章中说该变量提供的传播信息是定性的，其最大价值在于涡旋对平均流的反馈，即E矢量辐合处，西风风速降低。此外，E矢量水平分量与时间平均纬向风速的水平梯度的点乘与平均流和扰动场的局地正压能量转换率成正比，当点乘为正时，存在正的能量转换，通过从平均流向eddy的正压动量转换减弱纬向风场的不均一性。