红噪声是低频长波,其功率谱能量主要集中于低频处
白噪声是各个频率上的谱密度值相同
傅里叶变换
类似于谐波分析,将序列中的周期性视为正弦波
可以对数据做纬向傅里叶变换,也可以做时间上的傅里叶变换,得到傅里叶系数。常用的函数有以下三种
除以下三种外,还有基于复数时间序列的傅里叶变换 cfftf, cfftb ,当把其中的虚部数值设为0时,其计算结果类似于用 ezfftf,但用 ezfftf 时得到的频率只有正值,而用 cfftf 时可以得到负的频率值,适用于纬向数据,可以得到东传和西传的傅里叶系数,用该函数也可以对经傅里叶变换的傅里叶系数再进行傅里叶变换。
但用 cfftf 计算得到的结果没有标准化,若要得到标准化的结果,需要的输出结果再除以样本数
fourier_info
finfo = fourier_info(data, nhx, sclPhase) ;返回数组 finfo[3][...][N/2]
;对data的最右边一维做傅里叶变换,返回每个周期对应的振幅、第一个极大值的位置、方差百分比
;其中,振幅即每个周期对应的傅里叶系数的平方和的均方根
;设data最右边一维的长度为N,则分解得到的每个周期中包含的谐波数范围为 (0, N/2],谐波数值越大,周期越短。
;nhx=0时会返回谐波数分别为 (0, N/2] 时所对应的周期的信息,若 0 < nhx <= N/2,则返回谐波数分别为 (0, nhx] 时所对应的周期信息
;sclPhase其实就是data最右边一维点与点之间的间隔数,若最右边一维是经度,有72个点,则 sclPhase = 360/72 = 5
;注意点:data不能有缺测值,不包括周期点
;此外,该函数也有 fourier_info_n 的形式
ezfftf 向前快速傅里叶变换
cf = ezfftf(data) ;返回数组 [2][...][N/2]
;对data最右边一维做傅里叶变换,设其最右边一维的长度为N,返回傅里叶的实部与虚部系数
;同时以属性 xbar 返回data最右边一维的均值,以 npts 返回data最右边一维的长度,最右边一维不需要是2的倍数
;如果有缺测值,计算出来的傅里叶系数为0
ezfftb 向后快速傅里叶变换
其实就是根据傅里叶系数进行合成
data = ezfftb(cf, xbar)
;cf 即利用 ezfftf 生成的傅里叶系数,其最左边维的长度必须是2,且 cf(0,...) 为实部,cf(1,...) 为虚部
;xbar 是data最右边维的平均数,可以是一个数,也可以是一维数组,长度为 data 左边维数长度的乘积
;利用该函数及 ezfftf 函数可以提取出 data 前几个波数周期的合成
;或者只提取出其中一个波动的曲线
;设现在有一个 data (ntime, nlev, nlat, nlon)
cf = ezfftf (data) ;得到 cf (2, ntime, nlev, nlat, nlon/2)
cf(:,:,:,:,3:nlon/2) = 0.0
data_wave1_3 = ezfftb (cf, 0)
;重构的data_wave1-3的平均数为0
data_wave1_3 = ezfftb (cf, cf@xbar)
;重构的data_wave1-3的平均数为cf@xbar
功率谱分析
功率谱分析以傅里叶变换为基础,将时间序列的总能量分解到不同频率上的分量,根据不同频率波的方差贡献诊断出序列的主要周期,从而确定周期的主要频率。常用的函数有 specx_anal, 交叉功率谱 specxy_anal, 功率谱显著性检验specx_ci
功率谱分析的步骤:
- 原始数据处理,求距平,去趋势。求距平不会改变数据的总方差,但可以避免突变偏移量,因为在后续的分析步骤中一般会用0来扩充序列。而趋势会在频率为0的地方产生一个功率谱峰值,这个峰值会影响整个功率谱的分布,进而掩盖其他周期。The trend removal is performed first, then the trend-removed data are tapered. This combination minimizes “ringing” and “leakage”.
- 利用自相关系数或离散傅里叶变换计算粗谱估计。
- 由于光谱估计的高方差,原始周期图几乎没有直接的用处。原始周期图的波动可以由采样变异性驱动,这个问题在序列越短时就越严重。平滑原始周期图可以减少这个问题。如果用不同跨度的Daniell滤波器对原始周期图进行平滑处理,得到的结果是光谱表面更加平滑。置信区间更小。但是过度的平滑会模糊重要的光谱细节,而不充分的平滑会留下不稳定的不重要的光谱细节。
光谱估计的稳定性是“从一个序列的不同部分计算出的谱估计在多大程度上是一致的”或者“周期图中不相关的精细结构被消除的程度”。高稳定性对应于低方差的估计,是通过对多个周期图纵坐标求平均得到的。
在ncl中用 specx_anal 计算得到的功率谱值spcx随频率的积分等于序列方差,如下所示 (N是样本数,df=1/N是频率间隔)
(spcx(0)+spcx(N/2-1))*(df/2) + SUM{spcx(1:N/2-2)*df} = total variance of the series
对应spcx-frequency的曲线图中,曲线与横坐标所围面积即序列方差。由于大于10天的低频区域所占横坐标窄,对应的spcx虚假偏高。如果用周期作为横坐标,则spcx需要乘以对应频率的平方,才能保证曲线与横坐标所围面积依然是序列方差,但此时高频区域所占横坐标变窄,对应的方差密度 spcx*frq^2 偏高。那么用什么来作为横坐标能更好地表示每个周期对应地方差密度?根据下面ppt中的公式演算,认为用频率or周期的自然对数作为横坐标,能使横坐标的分布相对比较均匀,不会因横坐标范围的过度压缩,而产生虚高的方差密度。通过虚构有固定周期的序列,以往研究也表明这种方式能更好地凸显出序列的主要周期。
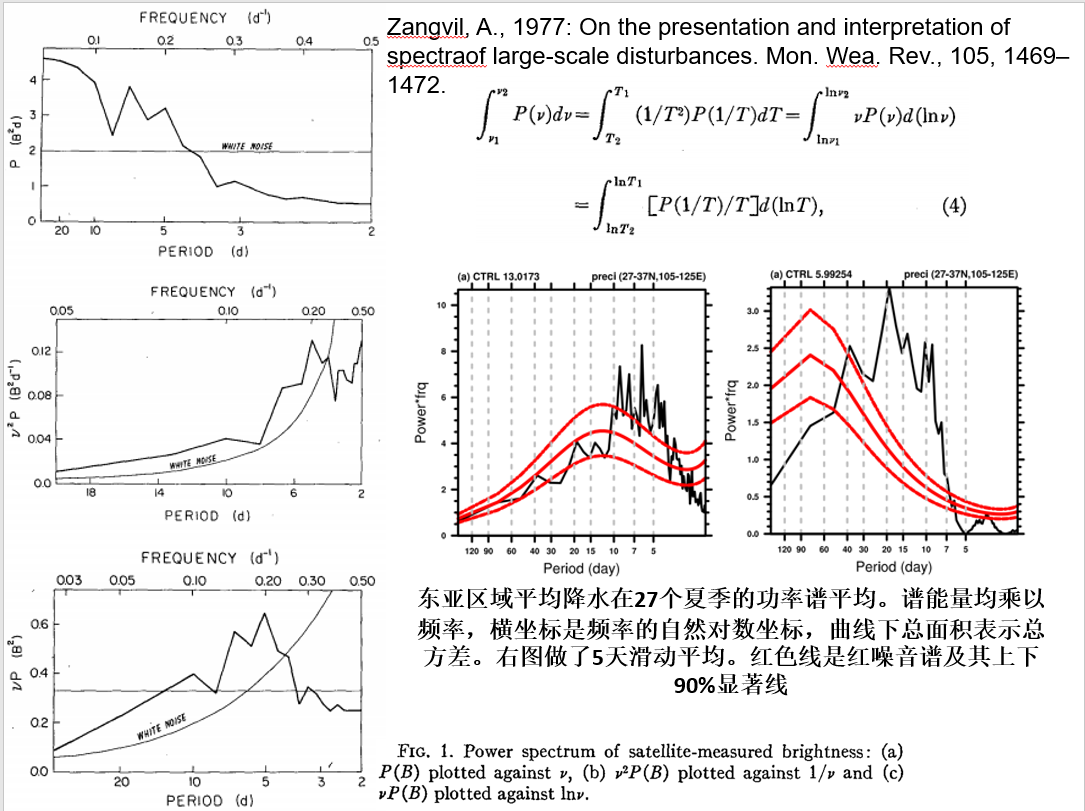
如果需要对27年每年夏季功率谱做气候态平均,此时马尔可夫显著线不是简单的27年的马尔可夫线平均,而是需要通过如下算法去计算(该算法摘自官网):
d = 0 ; detrending opt: 0=>remove mean 1=>remove mean + detrend
sm = 1 ; smooth: should be at least 3 and odd; if small than 3, it would do no smoothing
pct = 0.10 ; percent taper: (0.0 <= pct <= 1.0) 0.10 common. If pct =0.0, no tapering will be done. If pct = 1.0, the whole series is affected
;************************************************
; calculate mean spectrum spectrum and lag1 auto cor
;************************************************
; loop over each segment of length ntim
spcavg = new ( ntim/2, typeof(x))
spcavg = 0.0
r1zsum = 0.0
do nt=0,nyear-1
dof = specx_anal(x(nt,:),d,sm,pct) ; current segment spc
spcavg = spcavg + dof@spcx ; sum spc of each segment
r1 = dof@xlag1 ; extract segment lag-1
r1zsum = r1zsum + 0.5*log((1+r1)/(1-r1)) ; sum the Fischer Z
end do
r1z = r1zsum/nyear ; average r1z
r1 = (exp(2*r1z)-1)/(exp(2*r1z)+1) ; transform back
; this is the mean r1
spcavg = spcavg/nyear ; average spectrum
;************************************************
; Assign mean spectrum to data object
;************************************************
df = 2.0*nyear ; deg of freedom
df@spcx = spcavg ; assign the mean spc
df@frq = dof@frq
df@xlag1= r1 ; assign mean lag-1
splt = specx_ci(df, 0.05, 0.95) ; confidence interval
;splt(4,ntim/2) including input spectrum (indx=0), Markov Red Noise spectrum (indx=1),
;lower confidence bound for Markov (indx=2), upper confidence bound for Markov (indx=3)
Space-time Spectral Analysis
时空谱分析,主要用于研究热带波动。
带通滤波
ncl中的滤波主要有三种:
- 权重因子加滑动平均:用 ` filwgts_lanczos
函数产生权重,然后用wgt_runave_n_Wrap `结合上面产生的权重来进行滑动平均滤波。这种方法可以用于处理含缺测的数据,难点在于如何确定权重数的个数(必须是奇数)。当滤出的波段频率越低,需要的权重点数就越多,但这样会导致首尾的缺测数增多。因此可能需要重复计算以找出最佳的权重个数 - Butterworth带通滤波器:另一种是直接利用Butterworth带通滤波器
bw_bandpass_filter,这是一种信号处理滤波器,其设计目标是在通频带内具有尽可能平坦的频率响应。但该函数不能处理含缺测值的数据,因为它会把缺测值当正常数据处理,导致数值偏大最后超出数据范围。因此在使用该函数前,可以用linmsg_n函数,把缺测值都补上。其优点是在序列首尾的数据不会丢失。 - 利用傅里叶变换滤波:先用向前快速傅里叶变换
ezfftf函数得到傅里叶系数,然后将不需要的波段的系数设为0,再利用向后快速傅里叶变换ezfftb重构数据。该方法不会在首尾处产生缺测。但它无法对含有缺测值的序列进行运算。
此外还有专门用于空间滤波的函数 smth9
上述三种方法中,个人比较常用的是后两种。在计算EKE的时候,发现Butterworth带通滤波得到的EKE能量比基于傅里叶变换的带通滤波得到的EKE能量高很多,尤其是低频变率(10-90天)。于是特地对比了Butterworth带通滤波和基于傅里叶变换的带通滤波的时间序列(都去除了平均值),发现Butterworth带通滤波似乎保留了年循环的过程。
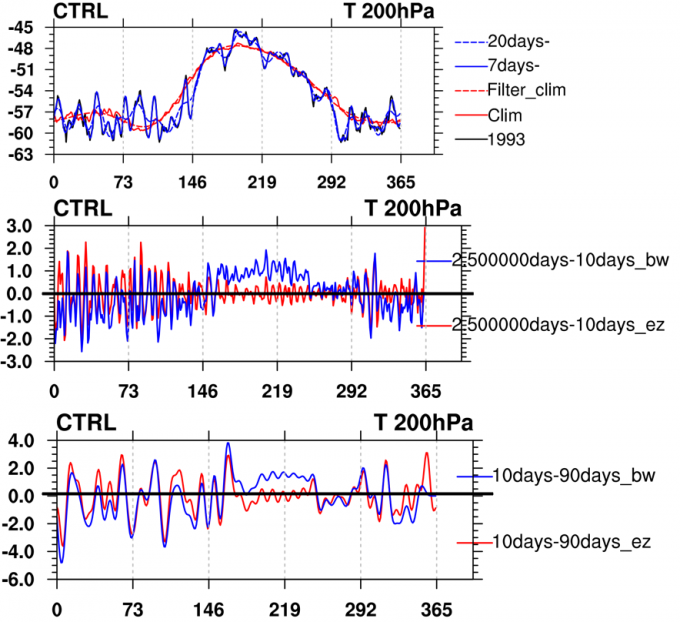
权重因子加滑动平均
利用 ` filwgts_lanczos `产生对称的权重因子时,该函数会以属性形式 wgt@freq, wgt@resp (一维数组,长度为 2*权重因子数nwgt+3) 返回该权重因子滤波的响应函数。响应函数图的绘制代码:
xyres = True
xyres@gsnMaximize = True
xyres@gsnFrame = False
xyres@tiMainString = "Band Pass: 20-100 srate=1: sigma = " + sigma
xyres@tiXAxisString = "frequency"
xyres@tiYAxisString = "response"
xyres@gsnLeftString = "fca=" + fca + "; fcb=" + fcb
xyres@gsnRightString = nWgt
xyres@trXMaxF = 0.1
xyres@trYMaxF = 1.1
xyres@trYMinF = -0.1
plot = gsn_csm_xy(wks, wgt@freq, wgt@resp, xyres)
X = (/0.0, fca, fca, fcb, fcb, 0.1/) ; ideal filter
Y = (/0.0, 0.0, 1.0, 1.0, 0.0, 0.0 /)
resGs = True
resGs@gsLineThicknessF = 1.0
gsn_polyline(wks,plot,X,Y,resGs)
不同权重因子数量对应的响应函数分布,其中矩形曲线即理想型的响应函数
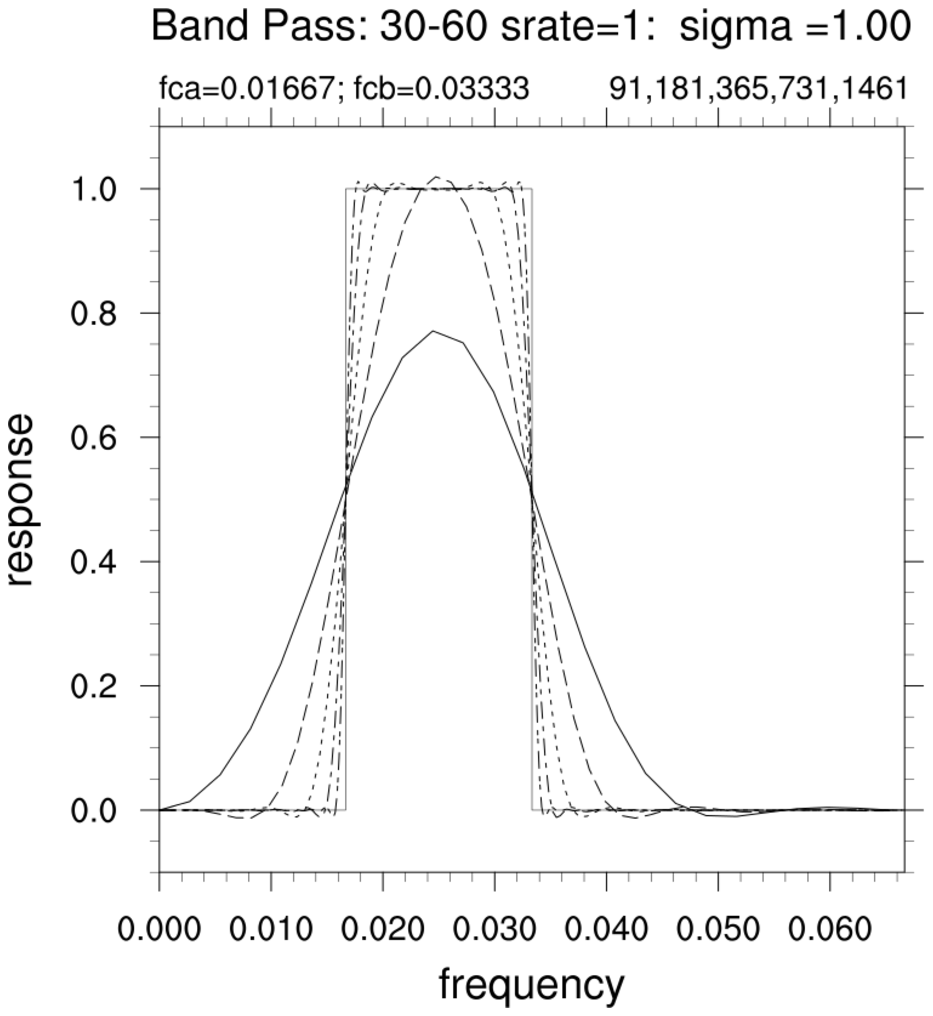
不同权重因子数的对比,蓝线(nwgt=49)和红线(nwgt=121)是24个月的滤波结果,绿线(nwgt=121)和黑线(nwgt=241)是120个月的低通滤波结果。
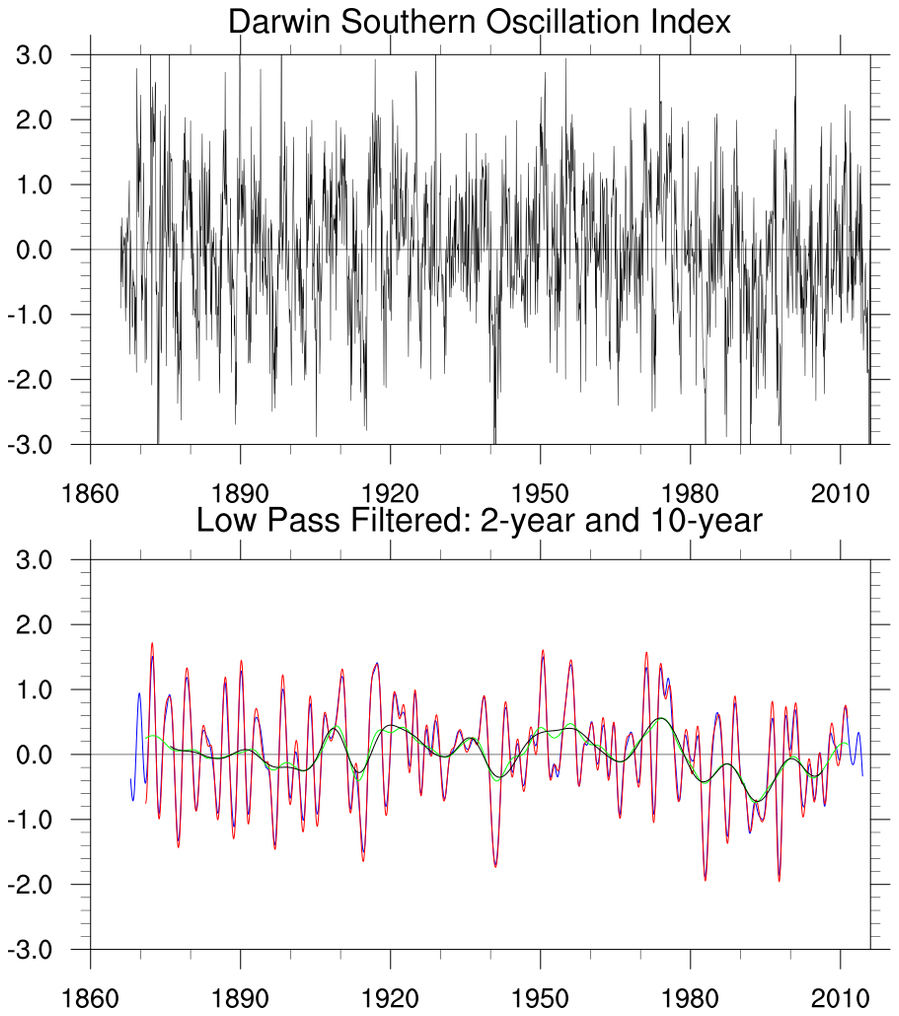
当第一种方法所使用的权重因子数越多,其结果与第二种带通滤波的结果类似,但会在首尾处产生很多缺测。
Butterworth带通滤波器
bw_bandpass_filter ( x, fca, fcb, opt, dims )
- x是需要滤波的数据列,可以是多维数组
- fca和fcb是滤波范围,一般是时间段的倒数,且两个都必须要小于0.5,按理来说fcb要大于fca,但大小关系反一下问题也不大
- opt是选项,默认情况下是用6阶滤波(opt@m=6),时间间隔为1(opt@dt=1),减去平均值(opt@remove_mean=True),输出滤波后的时间序列(opt@return_filtered=True),不输出滤波后的波包(opt@return_envelope=False)
不能处理含有缺测值的数据
ua = f->U_anom(:,{LAT},{LON}) ; ua(time), read from one grid point
ca = 50.0 ; band start (longer period)
cb = 40.0 ; band end (时间间隔不能等于2)
fca = 1.0/ca ; 'left' frequency
fcb = 1.0/cb ; 'right' frequency
dims = 0 ; 'time' dimension of ua
opt = True ; options to set
opt@return_envelope = True ; time series of filtered and envelope values
ua_bf = bw_bandpass_filter (ua,fca,fcb,opt,dims) ; (ua,fca,fcb,opt,dims)
copy_VarMeta(ua, ua_bf)
ua_bf@long_name = "Band Pass: "+cb+"-"+ca+" day"
计算得到的结果示意如下,其中上图是原始序列,下图是滤波后的时间序列(蓝色)与波包(红色)
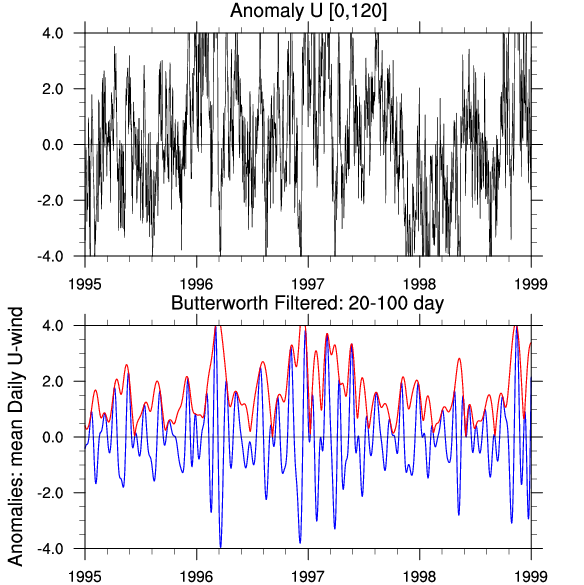
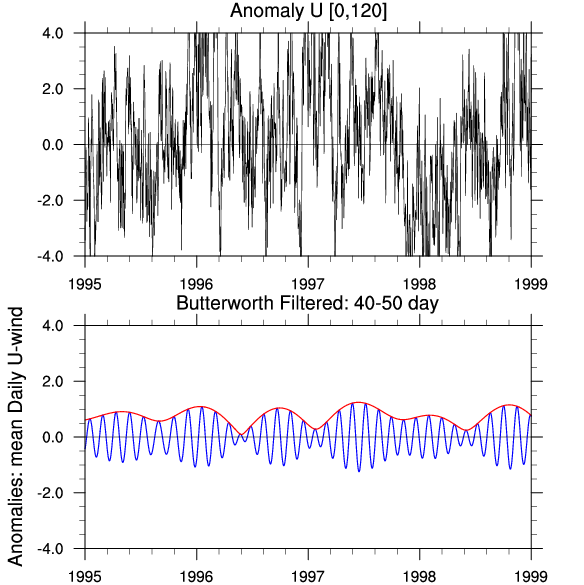
http://www.seismosoc.org/Publications/BSSA_html/bssa_96-2/05055-esupp/
 支付宝鼓励
支付宝鼓励  鸡腿鸡腿
鸡腿鸡腿