小波分析
利用小波分析,可以得到一个时间序列里任意周期的振幅及该振幅随时间变化的情况。
wave = wavelet(data, mother, dt, param, s0, dj, jtot, npad, noise, isigtest, siglvl, nadof) ;ncl用于小波分析的计算函数
- data,一维数组,用于进行小波分析的序列
- mother,整数,用于选择小波分析所使用的母小波函数,0 = Morlet,1 = Paul,2 = DOG (derivative of Gaussian), 若该值大于2或小于0,则默认为‘Morlet’,多数情况下都用Morlet
- dt,序列的时间间隔,多数情况下为1
- param,表示母小波函数的参数(必须大于0),若小于0 则使用默认值。
对于Morlet,该参数即波数,默认为6;对于Paul,改参数为order,默认为4;对于DOG,该参数为导数阶数,默认为2. - s0,能进行小波分析的最小规模,多数为2*dt。为了更精确地计算,对于Morlet,s0 = dt;对于Paul,s0 = dt/4。
- dj,离散尺度之间的间距,一般为0.25。该值越小,尺度分辨率越高,但计算更慢。
- jtot,整数,能分析的尺度数量,一般尺度取值范围为
s0至s0*2^[(jtot-1)*dj]。 因此,一般jtot = 1 + floattointeger( ( (log10(N*dt/s0)) /dj) /log10(2.) ) - npad,整数,用于小波分析的序列样本数
- noise,整数,0表示用白噪音进行显著性检验;1表示用红噪音进行显著性检验,多数情况下用1
- isigtest,整数,0表示do a regular chi-square(已假设时间序列满足正太分布,其平方,即功率谱,则满足卡方分布) test,1表示do a “time-average” test on the global wavelet spectrum
- siglvl,显著性检验水平,一般为0.05
- nadof,设为0,暂时忽略其作用
该函数运行后返回一数值类型同data的三维数组wave(2,jtot,npad),(0,:,:)是实部,(1,:,:)是虚部。该数组包含如下一些有用的属性:
- wave@power,功率谱,长为 jtot*npad 的一维数组,相当于
wave(0,:,:)^2 + wave(1,:,:)^2, 可通过power = onedtond (wave@power, (/jtot,npad/) )转换为二维数组 - wave@phase,位相,长为 jtot*npad 的一维数组,相当于 atan2(wave(1,:,:),wave(0,:,:))
- wave@signif,A one-dimensional array of length jtot containing significance levels versus scale. While power greater than this value, mean significant. 不同序列有不同的signif值。
- wave@gws,A one-dimensional array of length jtot containing the global wavelet spectrum.即某一周期的所有时间点的功率谱平均,类似于基于傅里叶变换的功率谱分析。
以下四个是单数值:
- wave@mean,用于小波分析序列的平均值
- wave@stdev,用于小波分析序列的标准差
- wave@lag1,A scalar containing the lag-1 autocorrelation of the input series.
- wave@r1,A scalar. If noise = 1(red noise background for significance testing), this contains the lag-1 autocorrelation of the input series. Otherwise, wave@r1 = 0.0. This is the value used in the significance test.
对于时间长度一样的序列,以下属性也相同:
- wave@scale,A one-dimensional array of length jtot containing the wavelet scales that were used.
scale = so*2^[(jtot-1)*dj]。对于Morlet母小波函数,scale与period相近。 - wave@period,A one-dimensional array of length jtot containing the “Fourier” periods (in time units) corresponding to “scale”.
- wave@coi,A one-dimensional array of length N containing the e-folding factor used for the cone of influence.是画边界区域必须的参数。
- wave@dof,A one-dimensional array of length jtot containing the degrees-of-freedom for significance test.似乎都是2.
- wave@cdelta,A scalar containing the constant “Cdelta” for the mother wavelet (Table 2 of reference).
- wave@psi0,A scalar containing the constant “psi(0)” for the mother wavelet (Table 2 of reference).
计算发现,输入的数据为原始值和用距平值算出来的结果是一样的。
但若用标准化数据计算的话,功率谱值会小很多。同时,用标准化数据计算的结果与用原始值计算的功率谱值(power)除以数据的方差的结果一样。
如果只是为了比较周期的变化,个人觉得用标准化数据计算的功率谱值便于在不同时间序列之间进行比较。因为有些地区的降水本来平均值就比较大,波动也就比较剧烈,因此气功率谱值就会比较大。
;计算显著性水平
SIG = power ; transfer metadata
SIG = power/conform (power,w@signif,0) ; >= 1 is significant
;计算无偏差的小波功率谱,可以突出小尺度的功率谱值
power = onedtond (wave@power, (/jtot,npad/) )
power_no_bias = power/conform(power,wave@scale,0)
gws_no_bias = wave@gws/wave@scale
;如何画边界区域的曲线
rescoi = True
rescoi@gsFillIndex = 1 ;确定填充类型
;只要是gs开头的属性均可设置,另外还可以设置gsFillColor,gsEdgeColor,gsEdgeDashPattern,gsEdgeThicknessF
plot = ShadeCOI(wks, plot, wave, data&time,rescoi)
其中函数 conform 是用于扩展数组的,其用法介绍如下
data = conform(x, r, ndim) ;将数组r扩充为和数组x同等大小的数组
;x,任何维数的数组
;r,一个值或一个数组,但这个数组必须是X的子集
;ndim,表明X的哪几维是与r相同的,若r是一个值,则ndim设为-1
无偏差的小波分析
Liu Y (2007),Rectification of the bias in the wavelet power spectrum,Journal of Atmospheric and Oceanic Technology, 24(12), 2093-2102.
若有一个序列包含有两个相同振幅的正弦波,但两者的频率不同, 那么传统的小波分析总是会使周期长、频率小的那个波动的功率谱大,但实际两者的功率谱应该是一样的。 这就是目前传统小波分析所存在问题。
为解决这一办法,传统的方法是滤去显著地低频波动,然后再做小波分析。现在也可以通过 wave@power/conform(power,wave@scale,0)来实现。
Torrence, C. and G. P. Compo, 1998: A Practical Guide to Wavelet Analysis
小波分析方法可以用来确定主要的变率周期及这些周期随时间的变化情况,应用广泛。遗憾的是,许多使用小波分析的研究无法给出明显的定量结果,目前主要都是定性的结果。这有部分是小波分析本身的错误,因为它涉及从一维时间序列(或频谱)到扩散的二维时频图像的转换。这种扩散情况由于任意的归一化方法和缺乏统计显著性检验而变得更加严重。本文的目的是提供一个简单易用的小波分析工具包,包括统计显著性检验。
- 小波分析 3.1 Windowed Fourier transform(WFT) 窗口傅里叶变换是用任意函数(例如boxcar, Gaussian window)在一个时间序列上滑动(滑动长度为T,时间步长dt),从而提取信号的局地频率信息。由于该分析过程中强加了一个尺度T(也叫响应间隔),WFT代表了一种不准确和低效的时频定位方法。不准确源于将未落于频率窗口中的高频和低频分量错误定位。低效来源于每个时间步都要对T/2dt频率进行分析,无论窗口大小或出现的主导频率如何。此外,需要尝试多种窗口长度以确定最合适的选择。对于由于主要频率范围太广而不能采用预定尺度的分析,应采用与尺度无关的时频局部化方法,如小波分析。
3.2 小波变换 小波变换可以用于分析在多个频率下都包含非平稳功率的时间序列。小波函数依赖于无量纲的时间参数,且其时间平均为0,时间和空间分布局地画。
术语“小波函数wavelet function”通常用于指正交小波或非正交小波。术语“小波基wavelet basis”仅指一个正交函数集。使用正交基意味着是离散小波转换,而非正交小波函数则可以是离散or连续小波转换。
小波分析的一个弊端是小波函数的任意选择。在选择小波函数时,需要考虑以下几个因子:
- 正交or非正交。在正交小波分析中,每个尺度的卷积次数和该尺度的wavelet basis宽度成正比。由此产生的小波频谱包含块状的小波能量,有利于信号处理,因为这给了信号更紧凑的代表。然而,对于时间序列分析,这种不定期的偏移会产生不同的小波频谱。相反,非正交分析在大尺度下是高度冗余的,相邻时间的小波谱是高度相关的,有利于时间序列的分析,能得到平滑、连续变化的小波振幅。
- 复数or实数形式。复数小波函数能同时返回振幅和位相信息,更适合捕捉振荡行为。实数小波函数只返回一个分量,可以用来分离峰值或不连续。可见如下例子:
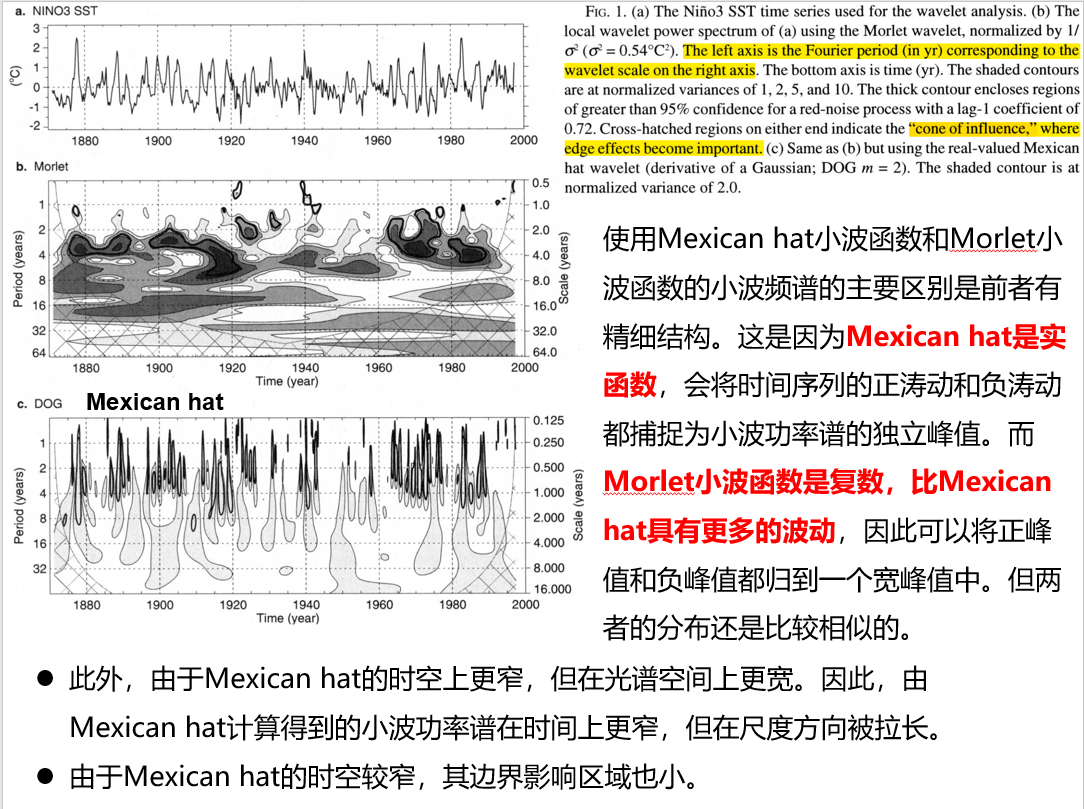
- 宽度。该文将小波函数的宽度定义为小波振幅的e-folding time。小波函数的分辨率受实际空间宽度和傅里叶空间宽度之间的平衡的影响。在时间上窄的函数有很好的时间分辨率,但频率分辨率减弱。在时间上宽的函数的时间分辨率弱,但频率分辨率高。
- 形状。小波函数应该反映时间序列中出现的特征类型。对于具有急剧跳跃或台阶的时间序列,人们会选择像Harr这样的boxcar函数,而对于平滑变化的时间序列,人们会选择平滑函数,如阻尼余弦。如果主要对小波功率谱感兴趣,那么小波函数的选择不是关键的,一个函数可以得到与另一个函数相同的定性结果。
四种常见的非正交小波函数有:Morlet,Paul,DOGs(m=2,6),如下图所示。 另外还有Haar,Daubechies这些正交小波函数。
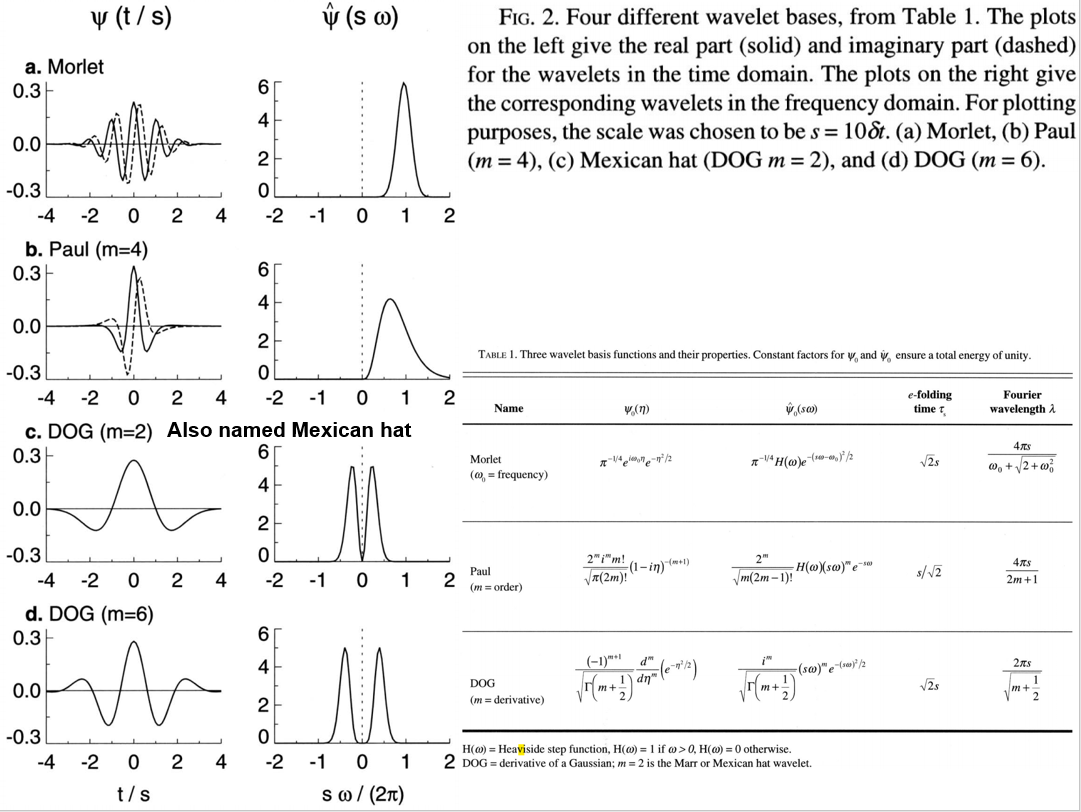
小波变换中的尺度选择也非常重要。对于正交小波,其尺度选择固定。但对于非正交小波分析,可以使用任意组合的尺度。
 支付宝鼓励
支付宝鼓励  鸡腿鸡腿
鸡腿鸡腿