    copy_VarMeta(var_from,var_to) ;最常用的一个函数，因为若变量的LAT和LON坐标若没有定义单位等要素，画map图会报错
    time := cd_calendar(time,option) ;将混合日期转换为公历日期，且option=0时，输出数据会多一维

显著性检验函数

0、Student’s t-distribution

下面的相关系数检验与样本均值检验都用到了学生t分布，都是先计算t统计量，然后根据t分布的概率密度函数计算 a two-tailed probability (prob)，若prob小于0.01，则说明其通过99%的显著性检验。

但当例如ncl的 regCoef_n 函数计算回归系数时，会将t统计量作为属性输出，此时若要对回归系数做显著性检验，就需要根据t统计量计算a two-tailed probability (prob)。

t分布的概率密度函数是：，其中参数v是自由度（一般等于样本数减2）。
T的概率密度函数的形状类似于均值为0方差为1的正态分布，但更低更宽。随着自由度的增加，则越来越接近均值为0方差为1的正态分布。

a two-tailed probability等于将t分布的概率密度函数从负无穷积到-t值得积分值加上从t积到正无穷的积分值。如下图阴影区域所示。

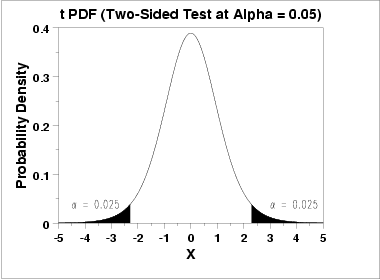
为此，ncl有两个函数来计算t统计值或probability。

; Calculates the t-value given the one-sided probability and the degrees of freedom.
     df = 16     ; t-value, 标量或数组
     p  = 0.025  ; degrees of freedom, 标量或与t相同维数的数组
     T = cdft_t(p, df)    ; T = -2.12
     p  = 0.975
     T = cdft_t(p, df)    ; T =  2.12

; Calculates the one-sided probability given a t-value and the degrees of freedom.
	t  = 2.12 ; t-value, 标量或数组
	df = 16   ; degrees of freedom, 标量或与t相同维数的数组
	P = cdft_p(-t, df)   ; P = 0.025  
	P = cdft_p( t, df)   ; P = 0.975 
	prob = 2*cdft_p(-t, df) ; a two-tailed probability

如果得到的t统计量是一个很大的数组且不确定其正负，此时可以用不完全beta函数计算。

; betainc(x,a,b) calculates the incomplete beta function ratio, which is the probability 
; that a random variable from a beta distribution having parameters a and b 
; will be less than or equal to x.

	t  = 2.12 ; t-value, 标量或数组
	df = 16   ; degrees of freedom, 标量或与t相同维数的数组
	prob = betainc( df/(df+t^2), df/2.0, 0.5)    ; prob=0.05

; betainc中输入的三个参数的维数要相同。
; 当输入的第一个参数有缺测时，得到的prob相应位置也是缺测

1、检验相关系数是否显著

rtest(相关系数r,样本数目n,0) # 用t分布检验相关系数是否显著，t=r*sqrt（（n-2）/（1-r**2））

返回统计概率值prob，当 prob.lt.0.01 时，说明其通过99%的显著性检验。上述n代表样本数，n-2 表示自由度。

除了用上述函数进行判断以外，也可以根据公式计算临界相关系数，当相关系数大于临界相关系数则通过显著性检验。而关于临界相关系数网上一般有表格可以查询，耶可以利用一些网站计算。更详细版相关系数检验临界值表

2、两组样本均值差异是否显著

ttest(均值1，方差1，样本数1，均值2，方差2，样本数2，iflag，tval_opt)

iflag，为True表示两组样本有相同的总值方差，为False表示有不同的总值方差

tval_opt，为True表示返回统计概率值和student_t值，为False则只返回统计概率

当统计概率值.lt.显著性水平siglvl（例如0.05），则两组样本差异显著

上图是计算两组样本均值是否有显著差异的t统计量，从中可以发现若两组样本的方差均为0或非常接近0时，该公式不成立，因此此时在ncl中设为缺测。但是在两组样本的方差都为0且均值有差异的情况下，这两组样本的均值一定是显著不同，但由于ncl将其设为缺测，此时会导致通过显著性检验的点减少，因此可以将方差无限趋近于0的值设为某个小量，例如0.01。(t值越大，通过显著性检验的可能性就越大）

var_vari = where(var_vari.le.0.000001.and.var_vari.ge.-0.000001,0.01,var_vari)

不过需要注意的是，对于散度、涡度等量级本身就非常小的物理量来说，其方差也非常小。如果用上述命令将无限趋于0的方差设为0.01，就会导致修改后的方差比实际的方差大很多，于是通过显著性检验的变量会减少。

个人觉得这个检验的原理是：当两组样本均值差异显著大于两组样本的平均标准差时，为通过显著性检验，即两组样本均值有显著差异。

3、检验两组样本的方差是否有显著差别

    ftest（方差1，样本数1，方差2，样本数2，0） ;F检验

返回统计概率值prob，用法同1,2

F统计值的计算方法如下：

计算EOF的函数

1、计算EOF特征空间模态

optEOF 		= True
optEOF@jopt = 1    # 1表示用相关矩阵计算EOFs，0表示用协方差矩阵计算EOFs（默认）
optEOF@pcrit= 50.0 # 0到100的浮点数
# 用以表示某一点的时间序列中的非缺测值需要达到50%以上才能计算EOF，否则该点设为缺测。
# 该值默认为50%。表明使用该函数可以有缺测。

neval		= n #计算前n个EOFs模态
eof	        = eofunc_n_Wrap(data,neval,optEOF,dim) #计算data的前neval个空间模态
# 该函数中的data可以是多维数组，除dim维外，其他维均会参与EOF。

# 假设现在有data(ntime,nlev,nlat,nlon)，若需要对每一层数据做EOF，则需要设置循环
eof     = new((/nlev,neval,nlat,nlon/),float)
eof_ts  = new((/nlev,neval,ntime/),float)
pcvar   = new((/nlev,neval/),float)
eval    = new((/nlev,neval/),float)
ts_mean = new((/nlev,neval/),float)
do nl = 0, nlev-1, 1
    eof_temp	= eofunc_n_Wrap(data(:,nl,:,:),neval,optEOF,0)
    eof_ts_temp = eofunc_ts_n_Wrap(data(:,nl,:,:),eof_temp,False,0) ;get the (neval,ntime)
    sig         = eofunc_north(eof_temp@pcvar,ntime,True)
    eof(nl,:,:,:)   = eof_temp                                 ;get the (nlev,neval,nlat,nlon) 
    eof_ts(nl,:,:) = dim_standardize_n_Wrap(eof_ts_temp,1,1)   ;get the (nlev,neval,ntime)
    pcvar(nl,:)    = eof_temp@pcvar
    eval(nl,:)     = eof_temp@eval
    ts_mean(nl,:)  = eof_ts_temp@ts_mean
end do

# 若EOF区域跨越的纬度较大，例如从30-70N，需要将data乘以一个系数再进行EOF，以弥补极地面积减小的变化。
pi   = atan(1.0)*4
wgt  = sqrt(cos( data&lat*pi/180.0 ))
data = data*wgt
eof	 = eofunc_n_Wrap(data, neval, optEOF, dim)

若输入的 data 为（time,nlat,nlon),则得到的为 eof(neval,nlat,nlon),且 eof 是标准化变量（每一空间模态的平方和=1），故空间模态的数值与变量本身的数值大小无关，即空间模态的数值本身无意义，一般只看其分布型。若想使其数值有意义，可通过乘上相应特征值的开方去标准化 eof(ne,:,:) = eof(ne,:,:)*sqrt( eof@eval(ne) ) ; units same as data ，对应的时间系数除以相应特征值的开方。

同时，该函数还会以属性形式返回：eval 特征值（一维数组），pcvar 特征值方差贡献（一维数组）。某一模态的特征值即该模态所有格点的方差和（用某格点数值乘以时间系数再求方差，然后所有格点求和），所有特征值之和就是原始场所有格点的方差和，也是时间系数（主分量）的方差。
此外，还有一个概念————模态局地方差贡献，就是某一模态在某个格点上的方差（用重构方法计算，不同格点的方差不同）对原始场该格点方差的比值。

用原始数据、距平值、标准化变量做EOF，得到的结果都不一样的。用相关矩阵计算EOFs得到的各模态特征值比用协方差矩阵计算得到的小很多，且两者的特征值方差贡献也完全不一样。一般ENSO的辨认是用距平值做EOF，也就是协方差矩阵。

当用相关矩阵计算EOFs时，相当于用标准化变量进行EOF分析，此时各个点的标准化变量可能相差不大，故能同时反映不同区域标准化变量的异常特征，反映的是变量场不同区域的相关情况.适合做分类、分型分析。用标准化变量做的EOF空间型中用值最大的那一点做一点相关图得到的相关图与该EOF空间型最相似，这也是EOF与一点相关图的相似性。
当用协方差矩阵计算EOFs时。相当于用距平变量进行EOF分析，此时EOF分析主要反映距平绝对值较大区域的主要异常特征
当用原始数据计算EOF时，主要空间分布型反映了平均状况，就相当于平均值，因此很少用原始数据做EOF，故该函数中也无这一选项

若研究的年际变率或年代际变率，EOF前需要进行相应的滤波操作，同时记得去趋势。

2、计算EOF各模态对应的时间系数

eof			= eofunc_n_Wrap(data,neval,optEOF,dim)
optETS		= True
optETS@jopt = 1 #指使用标准化数据矩阵计算时间序列，默认使用输入的data和eof（此时可设为False）
eof_ts		= eofunc_ts_n_Wrap(data,eof,optETS,dim) #计算与eof对应的时间序列

若输入的 data 为 (time,nlat,nlon), eof(neval,nlat,nlon),则得到 eof_ts（neval，time） (减去均值后的值），同时以属性的形式返回 ts_mean(neval),是 eof_ts 的均值

一般可以用这个时间序列做突变检验、功率谱分析、小波分析、趋势分析、相关计算等等，以衡量该典型空间场的时间变化特征。

3、检验各模态的特征值是否显著与其他特征值分离

sig = eofunc_north(eval特征值，时间样本数，prinfo) #也可用特征值的方差贡献pcvar做检验`

prinfo = True 时，依次打印计算所得的 delta lambda、特征值误差范围的最低界限、特征值、特征值误差范围的最高界限以及分离的显著性

输入的eval或者pcvar只能是一维数组，返回一维逻辑型数组，表示特征值是否显著与其他特征值分离

基于North. et al (1982): Sampling Errors in the Estimation of Empirical Orthogonal Functions.的文章对EOF模态进行显著性检验。公式如下 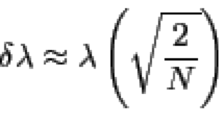lambda是特征值，N是数据的有效自由度，delta lambda是特征值的误差，将特征值加上或减去delta lambda得到特征值的误差范围，若前后两个特征值的误差范围有重叠，那么这两个特征值没有通过显著性检验。
函数eofunc_north打印出的最后两个数据就是特征值误差范围的最低和最高界限。

4、其他

EOF气象要素场重构的目的：

检验EOF是否正确
选取其中前几个主分量可还原气象要素场的大部分信息，也可以有选择性地还原气象要素场的特点信息

EOF气象要素场重构的应用：
研究印度洋海温时，若想要去除ENSO的信号，可以把印度洋和太平洋的SSTA做EOF，一般第一模态反映的就是ENSO的信号，然后重构第一模态（空间模态的每个格点乘以时间系数得到不同时刻该格点的不同值）则得到包含有ENSO信号的SSTA的序列场，原始场减去该序列场，则可消除与ENSO有关的SSTA。
当然要去除ENSO信号也可以通过回归的方法来做。

此外，除了对水平场做EOF外，也可以对垂直积分的水平场、纬向平均的垂直剖面或者纬向平均垂直平均的一维径向分布做EOF。还有将多个变量组合在一起做EOF的情况，例如MJO指数就是将近赤道径向平均的850 hPa、200hPa纬向风和OLR数据的组合场做EOF分析得到的第一模态和第二模态的主分量，且做EOF前已剔除年周期和年际变化分量。

ncl显著性检验函数和EOF函数